第3單元:史瓦西半徑
------本課程適合國中8年級以上------ 如果你把一物質壓縮得足夠小,最終就會得到一個黑洞,而且在一定的距離內,光再也無法逃脫,「史瓦西半徑」就是指任何物質都有的這個臨界距離的特徵半徑。對於一個典型的非旋轉黑洞而言,其史瓦西半徑即代表黑洞的大小,這是因為黑洞的大小被定義為連光也無法逃脫的範圍。黑洞的史瓦西半徑也被稱為「事件視界」。如果特定質量的物質被壓縮進入此半徑之內,則沒有任何已知的力量能夠阻止該物質由於自身的重力而壓縮成一個黑洞。因此,任何物體都可以計算出一個史瓦西半徑R,而大小取決於物質的質量M,史瓦西半徑的計算公式如下: c為光速:3×108 m/s(公尺/秒), G為萬有引力常數:6.67×10-11 N m2/kg2 (牛頓 公尺2/公斤2) 練習3-1: 計算一個70公斤的人的史瓦西半徑(公尺)。並用質子的直徑(約為10-15公尺)與答案做比較。 練習3-2: 計算木星的史瓦西半徑(公尺)。木星質量為1.9x1027公斤。 將此答案與練習2-4相比對。 練習3-3: 計算太陽的史瓦西半徑(公里)。太陽質量為1.99×1030公斤。 練習3-4: 由練習3-3的答案,我們可以化簡公式3-1。如果一物質的質量M以太陽質量為單位,史瓦西半徑R以公里為單位。則R = X M,試求係數X。 將此答案與練習2-3相比對。 練習3-5: 藉由練習3-4的答案,簡單計算銀河系的史瓦西半徑(公里)。假設銀河系質量約為太陽的2,500億倍。並用太陽系的半徑(假設為45億公里)與答案做比較。銀河系半徑及太陽系半徑皆為約略估算值。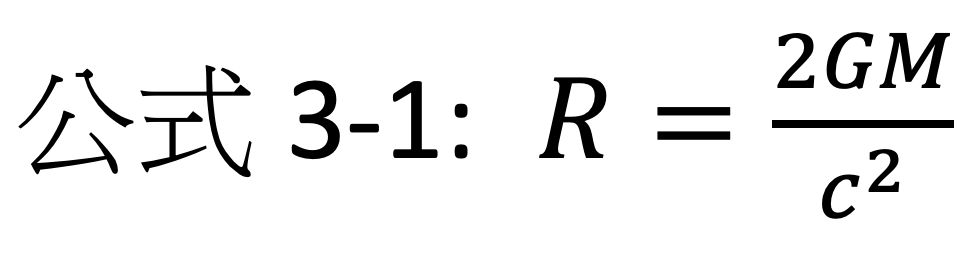

![我的E政府 [另開新視窗]](/images/egov.png)
