第7單元:時間膨脹效應
------本課程適合高中以上------ 根據愛因斯坦的狹義相對論,測量相對高速運動的慣系座標系統時,在該座標的時間會減慢,或稱為時間膨脹。時間膨脹效應的公式為: T為相對移動中的坐標系時間。 TO為相對靜止係測到相對移動中的坐標系時間。 c為光速。 而從廣義相對論的等效原理,我們可以把重力位能與動能的速度做相對應的轉換,即當你在距離質量M的黑洞中心距離為r的地方,速度v為: G為萬有引力常數:6.67×10-11 N m2/kg2 (牛頓 公尺2/公斤2) 當在質量M的黑洞的事件視界時,速度即為光速: R為黑洞的半徑。 將公式7-2、7-3帶入7-1,即得到: 從公式7-4得知,在距離黑洞越近的地方,時間過得越慢!而時間在事件視界上將靜止(無限膨脹)。 練習7-1: 請計算當你在距離一個太陽質量黑洞中心10公里的地方,相對於遠處靜止觀察者而言,時間膨脹效應是多少? 練習7-2: 假設現在有一艘太空船,從地球出發前往遠處的黑洞。請分別以地球的觀察者,以及太空船上的觀察者,描述太空船抵達黑洞之前的場景。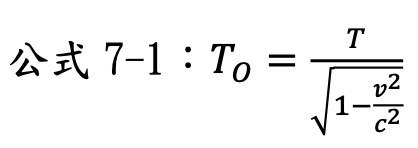
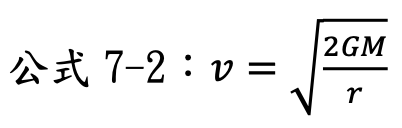
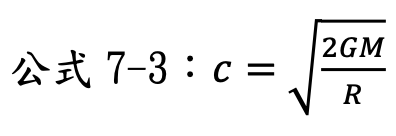
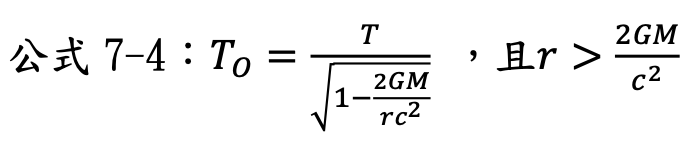

![我的E政府 [另開新視窗]](/images/egov.png)
